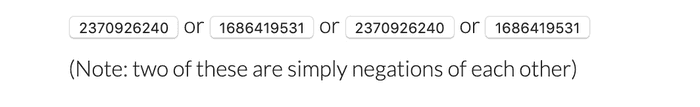Fair Coin Flip

Source

Link

This was a project for a number theory course (MATH 4150) I took at Georgia Tech. I picked this project and chose to write it in javascript for the browser because I liked the practical application of deciding a contest between two parties randomly and securely without any trusted third party. The implementation runs locally in a single browser using a toy number of bits to support user-input at each step walking-through the procedure. A practical application would take place between two browsers using a direct connection, limiting user-input to initiating procedure, and perhaps re-implemented in WebAssembly to support a higher number of bits for the keys to be secure.

Algorithm

Consider the two parties Bob and Alice.

1. Alice begins by generating two primes: p and q.

Ideally these primes would be large enough to be secure prime factors but for this implementation it defaults to five digits.

2. Alice sends Bob the product of the two primes: n = pq.

3. Bob then choses a number r, less than n to use as a square root mod n.

I gathered this input via a slider for free entropy.

4. Bob then squares r, r * r mod n = s and sends s to Alice.

At this point, Alice can use the knowledge of n's prime factors p and q to find all possible square roots of s mod n using Cipolla's algorithm Since n has two prime factors there will be four square roots, two of which are negations of each other. This follows from the Chinese remainder theorem. For looking up further on this s here is a quadratic residue.

5. Alice solves x * x = s mod n for roots a, -a, b, -b.

At this point, Alice does not know which of a or b is the root r that Bob used to generate s.

6. Alice sends one of the four roots to Bob.

Since Alice doesn't know which root was Bob's original root there's a 50/50 chance the root sent to Bob will be either the same one or its negation. In that case, Bob doesn't receive any new info. This means Alice wins the coin flip.

Otherwise if Alice sends a root that Bob doesn't know about, Bob now has all four roots and is able to derive both of n's prime factors p and q. Bob then sends p and q back to Alice to prove it and that means Bob wins the coin flip.

Implementation

The substantive parts of the implementation are to complete steps 1 and 5: generating the primes factors and solving for the square roots. I left the jQuery UI-wiring code in the index.html and pulled the more complex out to a separate js file.

Generating the prime factors was the most computationally expensive step of the procedure. I settled on an approximate algorithm to achieve reasonable performance. First, I used the Sieve of Eratosthenes to create a list of primes less than a million. I then used that list to do a first pass over a randomly generated number to check if it is a composite. Then, I used the Miller-Rabin test to decide if the number is prime. This is the overall procedure:

function generate_prime_of_length(n) {
  /* Returns a random prime' number that has n digits
   * where prime' means probably prime, uses Miller-Rabin
   */
  var p;
  while (true) {
    p = random_integer_of_length(n);
    if (!has_small_prime_factor(p) && miller_rabin_test(p, 100)) {
      return p;
    }
  }
}

The first step of using the sieve and a small prime list could undoubtedly has performance improvements, such as reducing use of the modulus operator or generating a larger prime list offline and storing it. But it was not the bottleneck of the procedure so I didn't try to optimize it further.

var has_small_prime_factor = (function () {
  /* anonymous function to trap list in scope to generate once */
  var small_prime = find_all_primes_less_than(1e6);
  var len = small_prime.length;
  return function (n) {
    /* Returns true if n has a factor in list of small primes */
    for (var i = 0; i < len; i++) {
      if (n % small_prime[i] === 0) {
        if (n == small_prime[i]) {
          /* quick check in case n is a small prime */
          return false; /* could handle small n better, but small so not necessary */
        }
        return true;
      }
    }
    return false;
  };
})();

Performance improvements probably exist in this function. Modulus can be an expensive call. However, this check was less expensive overall in the generation of primes, so I didn't try to optimize further.

The Miller-Rabin test on the other hand can take as much time as required for selected confidence. I went with a hundred iterations for a confidence of 1/4^100 = 6e-61 that the test returned a false positive.

function miller_rabin_test(n, k) {
  /* Returns false if n is composite and true if n is probably prime
   * with probability 1/4^k
   */
  var ds, d, s, a, x, i, j;
  ds = separate_two_factor(n - 1);
  d = ds[0];
  s = ds[1];
  witness: for (i = 0; i < k; i++) {
    a = random_integer_between(2, n - 2);
    x = modular_power(a, d, n);
    if (x == 1 || x == n - 1) {
      continue witness;
    }
    for (j = 0; j < s - 1; j++) {
      x = (x * x) % n;
      if (x == 1) {
        return false;
      }
      if (x == n - 1) {
        continue witness;
      }
    }
    return false;
  }
  return true;
}

The bottleneck of the Miller-Rabin test was the modular power routine which I also needed for step 5 of solving for the square roots so I spent some time trying to make that faster. To make the goal clear, here is a

function modular_power(b, k, n) {
  /* Returns b raised to the k in mod n */
  return Math.pow(b, k) % n;
}

I started with a less naive approach that better handled how I was using it with large powers.

function modular_power(b, k, n) {
  /* Returns b raised to the k in mod n */
  var ans = 1;
  for (var i = 0; i < k; i++) {
    ans = ans * b;
    if (ans > n) {
      ans = ans % n;
    }
  }
  return ans;
}

However, due to reliance on modulus and multiplication this approach was still not performant. After researching around I landed on this algorithm from yacas

function modular_power(b, k, n) {
  /* Returns b raised to the k in mod n */
  var p = b,
    j = k,
    r = 1;
  while (j > 0) {
    if ((j & 1) == 1) {
      // j is odd
      r = (r * p) % n;
    }
    p = (p * p) % n;
    j = j >> 1;
  }
  return r;
}

To clarify, let's reiterate that in pseudocode:

Input: positive integers base, power, and modulus
Note: assume all operations are mod the modulus (ie in Z modulus)
Let result := 1
While exponent > 0
  If exponent is odd then
    Multiply result by base
  Square base
  Integer divide exponent by 2
Return result

This reduces the time complexity from O(k) in the second approach to O(log k). It relies on the observation that the exponent, e, represented in binary is:

Therefore the base, b, raised to the exponent can be rewritten as:

Which is what we are calculating in the above pseudocode. When we check if the exponent is odd at each loop we are checking where $a_i$ is 1 or 0. If $a_i$ is 1 the exponent (at the ith iteration of the while loop) will be odd in which case we need to multiply our result by $b^{a_i} = b^1 = b$. Otherwise if $a_i = 0$ then $b^0 = 1$ which doesn't affect the product. Regardless of whether the exponent is odd at every iteration we need to account for the $b^{2^i}$ product which happens by progressively squaring the base.

The calculation to solve for the square roots of each prime put this faster modular exponentiation to good use:

function square_root_modp(a, p) {
  /* Returns a square root of a in mod p, p an odd prime, could be any
   * either root of the forms: x, p-x
   * (assumes a is indeed a quadratic residue)
   * First checks easy case of p=3(4) then uses Cipolla's algorithm:
   * http://people.math.gatech.edu/~mbaker/pdf/cipolla2011.pdf */
  var t, w, i, p2, x, y, x0, y0;
  if (p % 4 == 3) {
    return modular_power(a, Math.floor(p / 4) + 1, p);
  }
  do {
    t = random_integer_between(1, p);
    w = t * t - a;
  } while (jacobi(w, p) == 1);
  p12 = (p + 1) / 2;
  x = t; /* use x,y to track squaring: (t + root(w)) ^ k = x + y root(w) */
  y = 1; /* as such: t + root(w)) ^ k + 1 = xt + yw + (x + yt) root(w) */
  for (i = 1; i < p12; i++) {
    x0 = x * t + y * w;
    y0 = x + y * t;
    x = x0 % p;
    y = y0 % p;
  }
  if (x < 0) {
    x = x + p;
  }
  return x;
}